Convolution: 180 degree kernel before operation.
Cross-correlation problem, and need to normalized it.
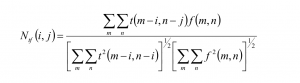
Harris-Laplace
SIFT
Convolution: 180 degree kernel before operation.
Cross-correlation problem, and need to normalized it.
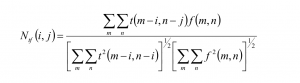
Harris-Laplace
SIFT
ALLOWED_HOSTSSECURE_HSTS_SECONDS=3600SECURE_HSTS_INCLUDE_SUBDOMAINS=TrueSECURE_CONTENT_TYPE_NOSNIFF=TrueSECURE_BROWSER_XSS_FILTER=TrueSECURE_SSL_REDIRECT=TrueSESSION_COOKIE_SECURE=TrueCSRF_COOKIE_SECURE=TrueX_FRAME_OPTIONS='DENY'SECURE_HSTS_PRELOAD=TrueStatic method, less objects
or check null by ourselves
Use StringBuffer instead of s=s+""
Static method, less objects
Normally distributed random variable with mean μ and variance σ²:
All higher order moments are given in terms of μ and variance σ².
Easily manipulated:
x ~ N(0, σx²) and y ~ N(0, σy²), then x + y ~ N(0, σx² + σy²)Central Limit Theorem:
For linear models:
Problems for nonlinear systems:
Characteristic scale
Normalize LOG
Use difference
{% csrf_token %}1.
LOGIN_URL='/login'LOGIN_REDIRECT_URL='/'2.
action="{% url 'django.contrib.auth.views.login' %}"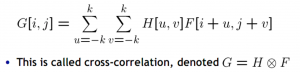
Convolution
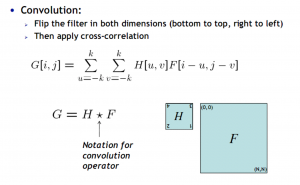
If H[-u,-v]=H[u,v], then correlation = convolution
1)Gaussian kernel
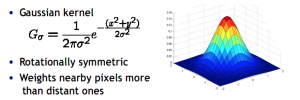
Gaussian smoothing:
Variance determines extent of smoothing
set filter half-width to about 3*variance
In Matlab:
hsize=10;
sigma=5;
h=fspecial(‘gaussian’ hsize,sigma);
mesh(h);imagesc(h);
outim=imfilter(im,h);
imshow(outim);
2)Oriented Gaussian Filters
3)Difference of Gaussian
DOG
Laplacian of Gaussian can be approximated by the difference between two different Gaussians
3)Derivative of Gaussian
LOG Laplacian of Gaussian

3.Sampling
wagen whell effect
Nyquist theorem: In order to recover a certain frequency f, we need to sample with at least 2f.
Representation of scale
The Gaussian pyramid
blur+subsample
The Laplacian Pyramid
a band pass representation vice a low pass representation of Gaussian
4.Detectors:Harris
Bolbs and conners
auto-correlation matrix
f(x+triangelex)=f(x)+trianglex*f'(x)+ trianglex^2*f”(x2)
5.Gaboe Wavelet
1.num2gray
(i>>1)^I
2.find rightest 1
x&(x-1)
3.find rightest 0
x&(x+1)
1.时间
http://www.cnblogs.com/emanlee/archive/2011/12/19/2293234.html
2.cell的访问:
1.X= C(s)使用这种"()"形式的返回的是cell类
2.X = C{s}使用这种"{}"形式的返回的是cell中的内容