CV_Filtering and Sampling
1.Correlation Filtering
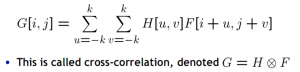
Convolution
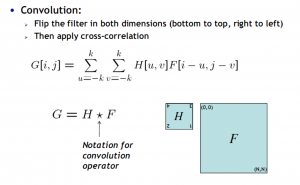
If H[-u,-v]=H[u,v], then correlation = convolution
2.
1)Gaussian kernel
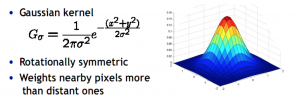
Gaussian smoothing:
Variance determines extent of smoothing
set filter half-width to about 3*variance
In Matlab:
hsize=10;
sigma=5;
h=fspecial(‘gaussian’ hsize,sigma);
mesh(h);imagesc(h);
outim=imfilter(im,h);
imshow(outim);
2)Oriented Gaussian Filters
3)Difference of Gaussian
DOG
Laplacian of Gaussian can be approximated by the difference between two different Gaussians
3)Derivative of Gaussian
LOG Laplacian of Gaussian

3.Sampling
wagen whell effect
Nyquist theorem: In order to recover a certain frequency f, we need to sample with at least 2f.
Representation of scale
The Gaussian pyramid
blur+subsample
The Laplacian Pyramid
a band pass representation vice a low pass representation of Gaussian
4.Detectors:Harris
Bolbs and conners
auto-correlation matrix
f(x+triangelex)=f(x)+trianglex*f'(x)+ trianglex^2*f”(x2)
5.Gaboe Wavelet